Trong chương trình học trung học phổ thông, lượng giác luôn được coi là môn học “khó nhằn” nhất đối với học sinh. Vậy có bao nhiêu công thức lượng giác và làm sao để nhớ hết được chúng?
Bacdau.vn sẽ tổng hợp tất cả các công thức một cách logic nhất cho các em.
Khái niệm cơ bản về lượng giác
Trước hết, lượng giác được hiểu là một chi nhánh trong toán học tìm hiểu và nghiên cứu chủ yếu về tam giác, mối quan hệ đối ứng của các góc trong hình tam giác và các cạnh của nó.
Ở chương trình học bậc phổ thông, các công thức lượng giác sẽ được biên soạn từ đơn giản tới nâng cao bao gồm: Công thức bậc cơ bản, Công thức biến đổi và công thức xác định nghiệm của phương trình lượng giác.
Các công thức lượng giác ở bậc học phổ thông
Công thức lượng giác của các cung đặc biệt
Khi giải toán đại số, các em sẽ dễ dàng bắt gặp các tam giác đặc biệt trong đó có các góc tạo thành các cung có tính chất riêng như cung đối nhau, cung phụ nhau, cung bù nhau,vv.. Với các trường hợp này, người ta đã nghiên cứu và đưa ra một số công thức cố định như sau:
Giá trị của một góc không đổi trong lượng giác:
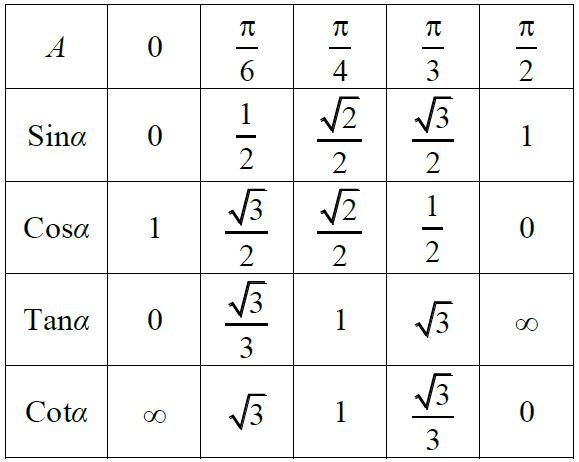
Công thức cố định

Thông thường để nhớ nhanh và hiệu quả công thức này các em có thể tự nhẩm câu cos đối, sin bù và hơn kém pi tang, kết hợp với áp dụng giải nhiều bài toán việc nhớ công thức lượng giác của các em sẽ rất dễ dàng.
Công thức cộng lượng giác
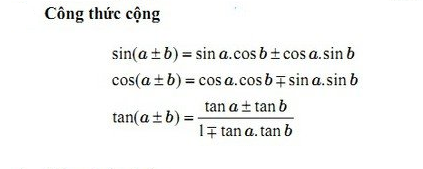
Các em nên lưu ý kỹ vì các góc trong lượng giác rất dễ nhầm. Sai góc đơn giản sẽ khiến việc tính toán sai hoặc không thể chứng minh được một bài toán.
Về phép cộng các em nhớ mẹo bằng cách nhớ mẹo cos+ cos là tích 2xCosxCos. Hiệu của cos là âm hai sin.
Công thức lượng giác chuyển tổng thành tích và chuyển tích thành tổng


Hai bảng công thức này luôn đi song hành với nhau và thường được dùng khi chứng minh hai góc là bù nhau hay phụ nhau trong tam giác nên khi học các em nên chú ý đồng thời cả hai để áp dụng hợp lý.

Phần này thường được giáo viên ưu ái cho vào các bài kiểm tra học một tiết và học kỳ bởi nó dễ nhớ, khó nhầm nên các em hãy học cho thật thuộc, đừng để mất điểm nhé.
Công thức tính nghiệm trong một phương trình đơn giản

Đúng với tên gọi của nó công thức này áp dụng trong giải các phương trình. Với những dạng bài giải phương trình lượng giác phổ thông, bậc cao nhất thường là bậc 2, hai đến 3 ẩn, dạng này các em nên chú ý đặt x để giải.
Ngoài ra nếu yêu thích bộ môn đại số hoặc trong đội tuyển thi học sinh giỏi các cấp thì các em nên tham khảo thêm về công thức tính hàm lượng giác ngược cũng như tích vô hạn trong lượng giác.
Trên đây là những thông tin hữu ích nhất cho các em trong giải các bài toán cần sử dụng công thức lượng giác. Mong rằng nó có thể giúp các em học tập hiệu quả hơn.
Các em cũng có thể tham khảo thêm bài toán về tam giác vuông, tam giác cân và tam giác đều trong trang.
